


Next: Refinement
Up: Least-Squares Fitting of a
Previous: Definition of problem
We begin with the constraint that the adjusted points  are
required to satisfy the hyperplane equation, i.e.
are
required to satisfy the hyperplane equation, i.e.
 where
where  is as defined in Equation (2).
Defining residuals
is as defined in Equation (2).
Defining residuals
 allows this constraint
to be rewritten as
allows this constraint
to be rewritten as
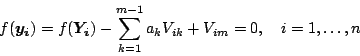 |
(4) |
Now, given any values of the parameters  , we seek those values of
, we seek those values of
 that will minimize
that will minimize  for that choice of the
for that choice of the  , subject
to the constraint (4). Thus we require
, subject
to the constraint (4). Thus we require
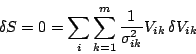 |
(5) |
From (4) we have
 |
(6) |
Multiplying each of the  equations (6) by its own
undetermined multiplier
equations (6) by its own
undetermined multiplier  and adding them all to
Equation (5), we obtain
and adding them all to
Equation (5), we obtain
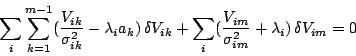 |
(7) |
Since the  are independent, the coefficients of
are independent, the coefficients of  in this equation must individually be zero, giving
in this equation must individually be zero, giving
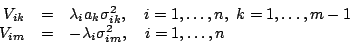 |
(8) |
Substituting this result into Equation (4) and
solving for  yields
yields
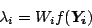 |
(9) |
where
![\begin{displaymath}
W_i = \left[ \sum_{k=1}^{m-1} a_k^2 \sigma_{ik}^2 + \sigma_{im}^2
\right]^{-1}
\end{displaymath}](img45.gif) |
(10) |
This allows  to be rewritten as
to be rewritten as
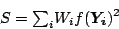 |
(11) |
This expresses  in the form of a weighted sum of the
residuals as defined for a conventional regression, but with weights
that properly take account of the individual uncertainties
in the form of a weighted sum of the
residuals as defined for a conventional regression, but with weights
that properly take account of the individual uncertainties
 . Now
. Now  is to be minimized with respect to the
parameters
is to be minimized with respect to the
parameters  . Setting
. Setting
 leads to the
following set of equations analogous to the normal equations of the
conventional regression:
leads to the
following set of equations analogous to the normal equations of the
conventional regression:
![\begin{displaymath}
\begin{array}{l}
\sum_i W_i f(\vec{Y_i}) y_{ik} = 0, \quad k=1, \ldots, m-1 [1ex]
\sum_i W_i f(\vec{Y_i}) = 0
\end{array}\end{displaymath}](img48.gif) |
(12) |
Since the parameters  occur in
occur in  ,
,  , and
, and
 , these equations are nonlinear and cannot be solved in
closed form. However, recognizing that
, these equations are nonlinear and cannot be solved in
closed form. However, recognizing that  and
and  are
only weakly dependent on the parameters of the hyperplane, we can
linearize Equations (12) by treating those quantities as
constants. Writing out
are
only weakly dependent on the parameters of the hyperplane, we can
linearize Equations (12) by treating those quantities as
constants. Writing out  in terms of the parameters, then, we
obtain
in terms of the parameters, then, we
obtain
 |
(13) |
Identifying the parenthesized terms in
Equation (13) as the elements of an  matrix
matrix  and the right-hand sides as elements of a vector
and the right-hand sides as elements of a vector  of length
of length  , this set of equations is seen as a linear system of the
form
, this set of equations is seen as a linear system of the
form
 . Solution proceeds iteratively. Starting
with an initial guess for the vector of coefficients
. Solution proceeds iteratively. Starting
with an initial guess for the vector of coefficients  , the
matrix
, the
matrix  and vector
and vector  are evaluated and the system
are evaluated and the system
 is solved for the new value of
is solved for the new value of  . This new
value is used to re-evaluate
. This new
value is used to re-evaluate  and
and  , and the equation is
solved again. The
iteration is continued until convergence is obtained. In practice, it
is not necessary to have a good starting guess for
, and the equation is
solved again. The
iteration is continued until convergence is obtained. In practice, it
is not necessary to have a good starting guess for  . From
Equation (10) it can be seen that the initial choice
. From
Equation (10) it can be seen that the initial choice  gives, as the result of the first iteration, the same parameters as
would be obtained if the
gives, as the result of the first iteration, the same parameters as
would be obtained if the  were zero for all
were zero for all  except
except  . This is the same result as would be given by the
conventional weighted regression of
. This is the same result as would be given by the
conventional weighted regression of  against the other
coordinates. Incidentally, this means that weighted averages (
against the other
coordinates. Incidentally, this means that weighted averages ( )
are computed correctly in one iteration. Experience has shown that
the convergence is rapid for data
sets where the fit is justified, and only a few iterations are
necessary to obtain the coefficients to accuracies that are well
within their uncertainties.
)
are computed correctly in one iteration. Experience has shown that
the convergence is rapid for data
sets where the fit is justified, and only a few iterations are
necessary to obtain the coefficients to accuracies that are well
within their uncertainties.
Subsections



Next: Refinement
Up: Least-Squares Fitting of a
Previous: Definition of problem
Robert Moniot
2002-10-20
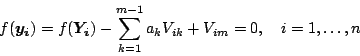
![]() occur in
occur in ![]() ,
, ![]() , and
, and
![]() , these equations are nonlinear and cannot be solved in
closed form. However, recognizing that
, these equations are nonlinear and cannot be solved in
closed form. However, recognizing that ![]() and
and ![]() are
only weakly dependent on the parameters of the hyperplane, we can
linearize Equations (12) by treating those quantities as
constants. Writing out
are
only weakly dependent on the parameters of the hyperplane, we can
linearize Equations (12) by treating those quantities as
constants. Writing out ![]() in terms of the parameters, then, we
obtain
in terms of the parameters, then, we
obtain