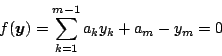 |
(2) |
The measured data consist of a set of ![]() vectors
vectors
![]() . Each coordinate
. Each coordinate ![]() of each data point has an
associated experimental uncertainty
of each data point has an
associated experimental uncertainty ![]() . (The
. (The ![]() may or may not be known a priori. We assume that at least their
relative magnitudes are known.) The experimental errors will cause
the data points
may or may not be known a priori. We assume that at least their
relative magnitudes are known.) The experimental errors will cause
the data points ![]() to lie scattered off the hyperplane of
Equation (2). Therefore one seeks a ``best fit''
to the data.
to lie scattered off the hyperplane of
Equation (2). Therefore one seeks a ``best fit''
to the data.
The method of principal component analysis, referred to above, is equivalent to seeking the hyperplane that minimizes the sum of squares of perpendicular distances from the measured points to the hyperplane. As already mentioned, this method is unable to take proper account of the experimental uncertainties of the data, and is not invariant under a change of scale of one or more axes.
The usual method that one finds in the literature for obtaining a best
fit of this kind is based on minimizing a sum of squares of the
residuals ![]() . This is called a regression of
. This is called a regression of ![]() against
against ![]() through
through ![]() . The sum of squares of these
residuals is either unweighted or weighted by
. The sum of squares of these
residuals is either unweighted or weighted by
![]() (Bevington, 1991). This approach ignores the uncertainties in
coordinates
(Bevington, 1991). This approach ignores the uncertainties in
coordinates ![]() through
through ![]() . It also gives different results
depending on which coordinate is chosen as the ``dependent''
coordinate
. It also gives different results
depending on which coordinate is chosen as the ``dependent''
coordinate ![]() .
.
The correct treatment that properly takes account of the experimental
uncertainties was formulated by Deming (1943). Given the data
![]() with associated uncertainties
with associated uncertainties ![]() , a set of
corresponding ``adjusted'' values
, a set of
corresponding ``adjusted'' values ![]() are sought which lie
exactly on the hyperplane (2) and minimize the
variance
are sought which lie
exactly on the hyperplane (2) and minimize the
variance